This document is a continuation of WebAssembly and WebGPU enhancements for faster Web AI, part 1. We recommend you read this post or watch the talk at IO 24 before continuing.
WebGPU
WebGPU gives web applications access to the client's GPU hardware to perform efficient, highly-parallel computation. Since launching WebGPU in Chrome, we've seen incredible demos of artificial intelligence (AI) and machine learning (ML) on the web.
For example, Web Stable Diffusion demonstrated that it was possible to use AI to generate images from text, directly in the browser. Earlier this year, Google's own Mediapipe team published experimental support for large language model inference.
The following animation shows Gemma, Google's open source large language model (LLM), running entirely on-device in Chrome, in real time.
The following Hugging Face's demo of Meta's Segment Anything Model produces high quality object masks entirely on the client.
These are just a couple of the amazing projects which showcase the power of WebGPU for AI and ML. WebGPU allows these models and others to run significantly faster than they could on the CPU.
Hugging Face's WebGPU benchmark for text embedding demonstrates tremendous speedups as compared to a CPU implementation of the same model. On an Apple M1 Max laptop, WebGPU was over 30 times faster. Others have reported that WebGPU accelerates the benchmark by over 120 times.
Improving WebGPU features for AI and ML
WebGPU is great for AI and ML models, which can have billions of parameters, thanks to support for compute shaders. Compute shaders run on the GPU and help run parallel array operations on large volumes of data.
Among the numerous improvements to WebGPU in the past year, we've continued to add more capabilities to improve ML and AI performance on the web. Recently, we launched two new features: 16-bit floating point and packed integer dot products.
16-bit floating point
Remember, ML workloads don't require precision. shader-f16 is a feature that enables use of the f16 type in WebGPU shading language. This floating point type takes up 16 bits, instead of the usual 32 bits. f16 has a smaller range and is less precise, but for many ML models, this is sufficient.
This feature increases efficiency in a few ways:
Reduced memory: Tensors with f16 elements take up half the space, which cuts memory use in half. GPU computations are often bottlenecked on memory bandwidth, so half the memory can often mean shaders run twice as fast. Technically, you don't need f16 to save on memory bandwidth. It's possible to store the data in a low-precision format, and then expand it out to full f32 in the shader for computation. But, the GPU spends extra computing power to pack and unpack the data.
Reduced data conversion: f16 uses less compute by minimizing data conversion. Low precision data can be stored and then used directly without conversion.
Increased parallelism: Modern GPUs are able to fit more values simultaneously in the GPU's execution units, allowing it to perform a greater number of parallel computations. For example, a GPU that supports up to 5 trillion f32 floating-point operations per second might support 10 trillion f16 floating-point operations per second.
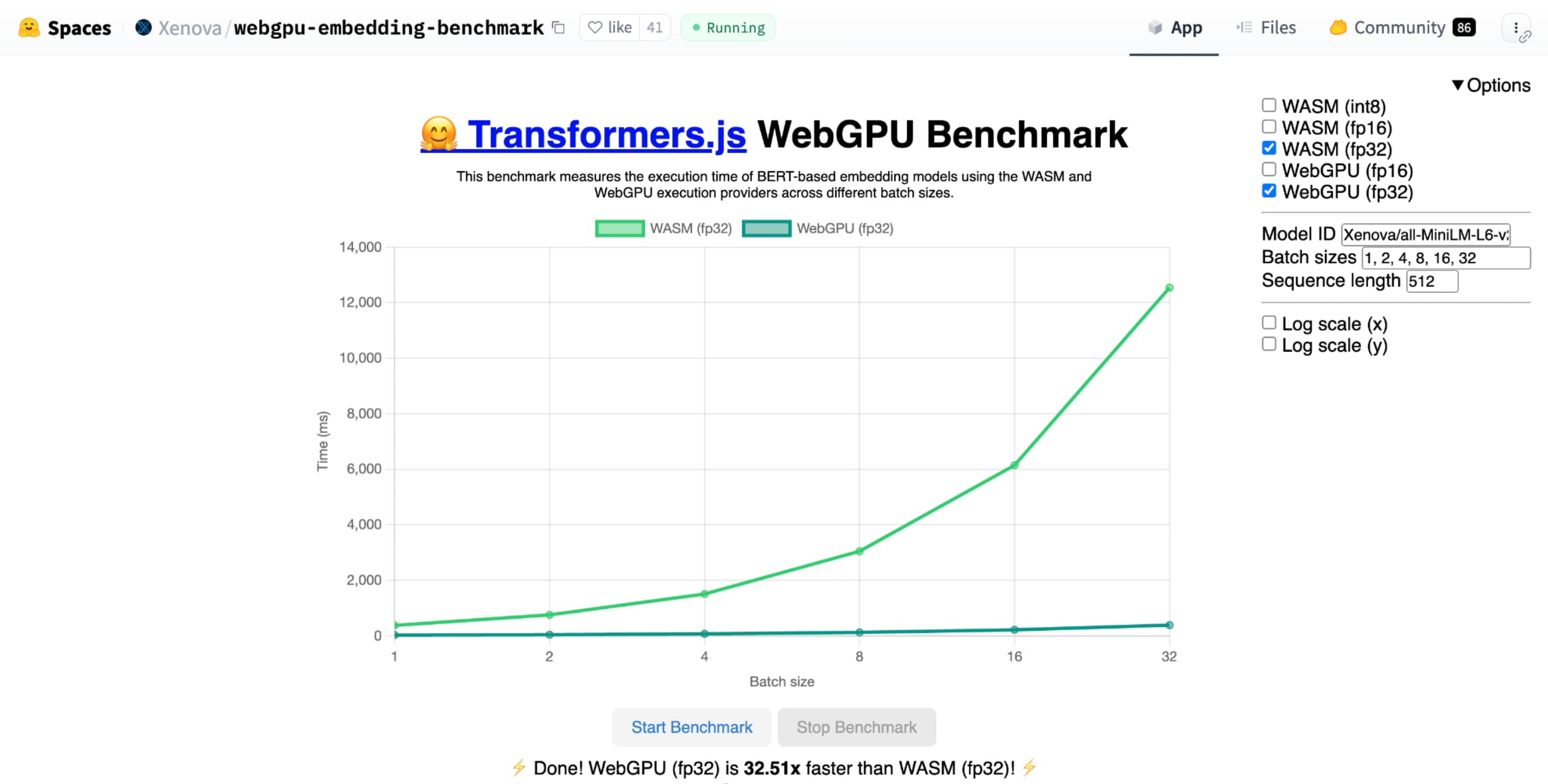
shader-f16, Hugging Face's WebGPU benchmark for text embedding benchmark runs the benchmark 3 times faster than f32 on Apple M1 Max laptop.
WebLLM is a project which can run multiple large language models. It uses Apache TVM, an open source machine learning compiler framework.
I asked WebLLM to plan a trip to Paris, using the Llama 3 eight-billion parameter model. The results show that during the prefill phase of the model, f16 is 2.1 times faster than f32. During the decode phase, it's over 1.3 times faster.
Applications must first confirm that the GPU adaptor supports f16, and if it's available, explicitly enable it when requesting a GPU device. If f16 isn't supported, you can't request it in the requiredFeatures array.
// main.js
const adapter = await navigator.gpu.requestAdapter();
const supportsF16 = adapter.features.has('shader-f16');
if (supportsF16) {
// Use f16.
const device = await adapter.requestDevice({
requiredFeatures: ['shader-f16'],
});
initApp(device);
}
Then, in your WebGPU shaders, you must explicitly enable f16 at the top. After that, you're free to use it within the shader like any other float data type.
// my-shader.wgsl
enable f16;
struct Data {
values : array<vec4<f16>>
}
@group(0) @binding(0) var<storage, read> data : Data;
@compute @workgroup_size(64) fn main(@builtin(global_invocation_id) gid : vec3u) {
let value : vec4<f16> = data.values[gid.x];
...
}
Packed integer dot products
Many models still work well with just 8 bits of precision (half of f16). This is popular among LLMs and image models for segmentation and object recognition. That said, the output quality for models degrades with less precision, so 8-bit quantization isn't suitable for every application.
Relatively few GPUs natively support 8-bit values. This is where packed integer dot products come in. We shipped DP4a in Chrome 123.
Modern GPUs have special instructions to take two 32-bit integers, interpret them each as 4 consecutively-packed 8-bit integers, and compute the dot product between their components.
This is particularly useful for AI and machine learning because matrix multiplication kernels are composed of many, many dot products.
For example, let's multiply a 4 x 8 matrix with an 8 x 1 vector. Computing this involves taking 4 dot products to calculate each of the values in the output vector; A, B, C, and D.
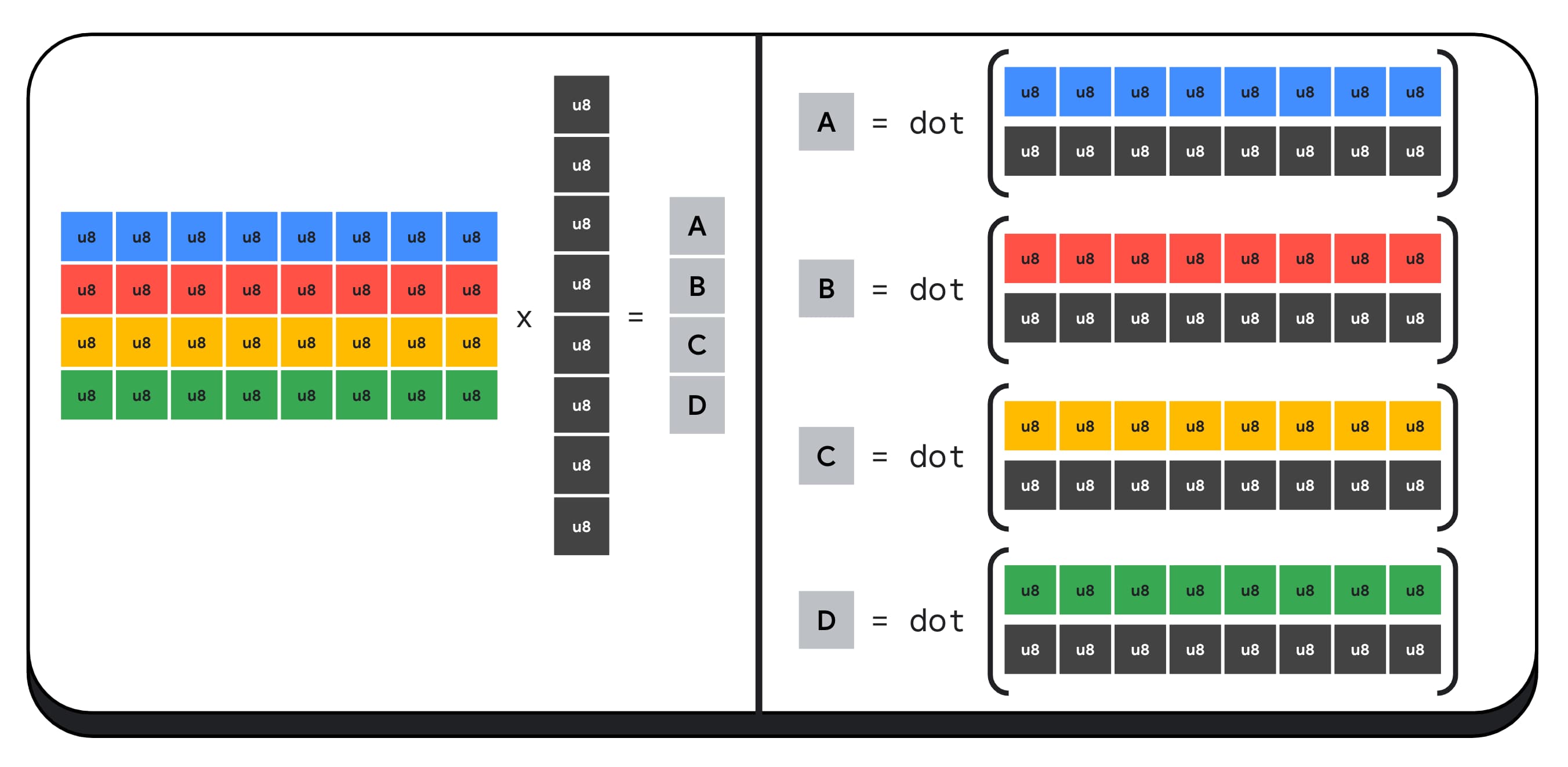
The process to compute each of these outputs is the same; we'll look at the steps involved in computing one of them. Before any computation, we'll first need to convert the 8-bit integer data to a type we can perform arithmetic with, such as f16. Then, we run an element-wise multiplication and finally, add all the products together. In total, for the entire matrix-vector multiplication, we perform 40 integer to float conversions to unpack the data, 32 float multiplications, and 28 float additions.
For larger matrices with more operations, packed integer dot products can help reduce the amount of work.
For each of the outputs in the result vector, we perform two packed dot product operations using the WebGPU Shading Language built-in dot4U8Packed, and then add the results together. In total, for the entire matrix-vector multiplication, we don't perform any data conversion. We execute 8 packed dot products and 4 integer additions.

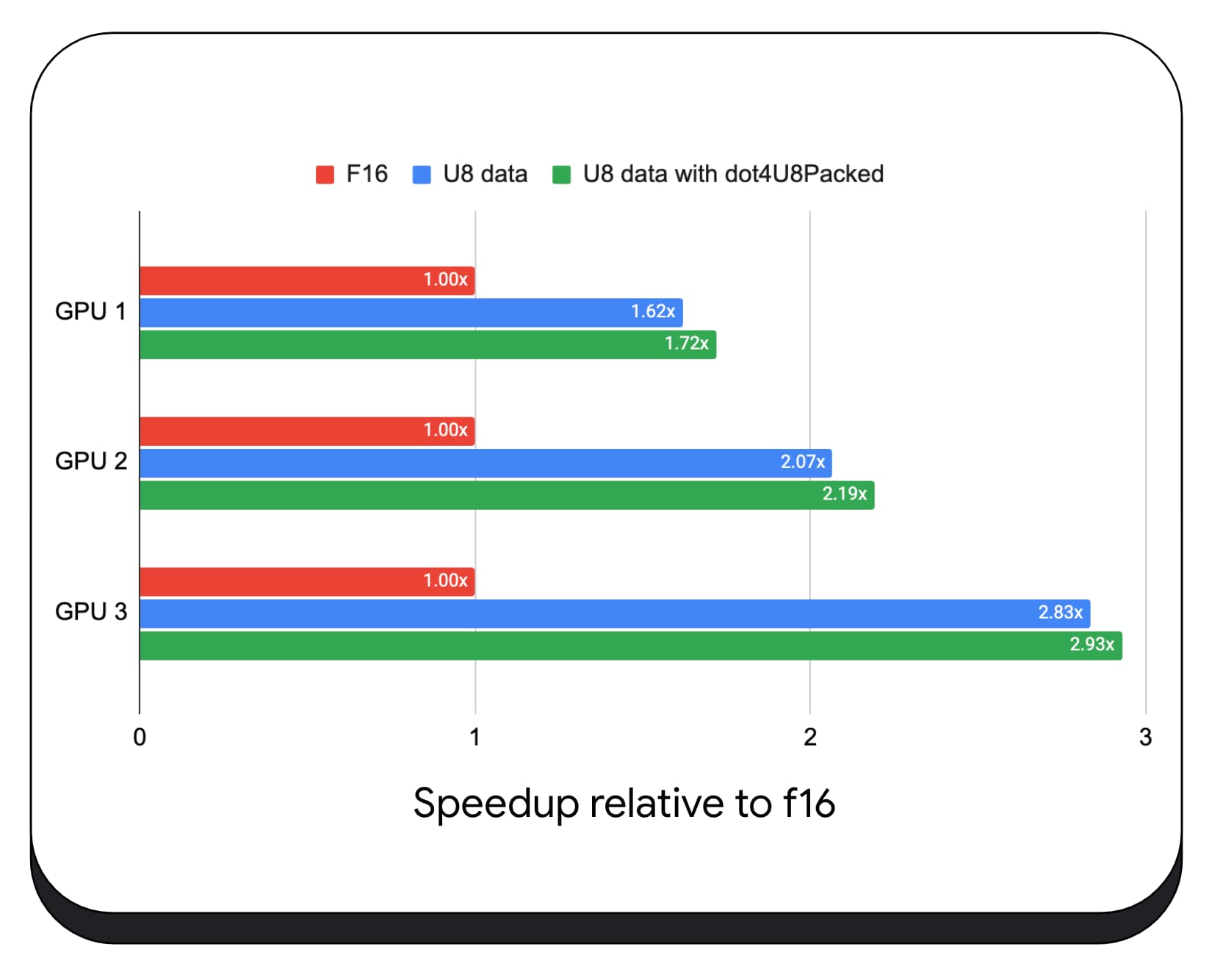
We tested packed integer dot products with 8-bit data on a variety of consumer GPUs. Compared to 16-bit floating point, we can see that 8-bit is 1.6 to 2.8 times faster. When we additionally use packed integer dot products, the performance is even better. It's 1.7 to 2.9 times faster.
Check for browser support with the wgslLanguageFeatures property. If the GPU doesn't natively support packed dot products, then the browser polyfills its own implementation.
// main.js
if (navigator.gpu.wgslLanguageFeatures.has('packed_4x8_integer_dot_product')) {
// Use dot4U8Packed, dot4I8Packed builtin
// functions in the shaders.
}
The following code snippet diff (difference) highlighting the changes needed to use packed integer products in a WebGPU shader.
Before — A WebGPU shader that accumulates partial dot products into the variable `sum`. At the end of the loop, `sum` holds the full dot product between a vector and one row of the input matrix.
// my-dot-product.wgsl @compute @workgroup_size(64) fn main(@builtin(global_invocation_id) gid : vec3u) { var sum : f16; let start = gid.x * uniforms.dim; for (var i = 0u; i < uniforms.dim; i++) { let v1 : vec4<f16> = vector.values[i]; let v2 : vec4<f16> = matrix.values[start + i]; sum += dot(v1, v2); } }
After — A WebGPU shader written to use packed integer dot products. The main difference is that instead of loading 4 float values out of the vector and matrix, this shader loads a single 32-bit integer. This 32-bit integer holds the data of four 8-bit integer values. Then, we call dot4U8Packed to compute the dot product of the two values.
// my-dot-product.wgsl
@compute @workgroup_size(64)
fn main(@builtin(global_invocation_id) gid : vec3u) {
var sum : f32;
let start = gid.x * uniforms.dim;
for (var i = 0u; i < uniforms.dim; i++) {
let v1 : u32 = vector.values[i];
let v2 : u32 = matrix.values[start + i];
sum += dot4U8Packed(v1, v2);
}
}
Both 16-bit floating point and packed integer dot products are the shipped features in Chrome that accelerate AI and ML. 16-bit floating point is available when the hardware supports it, and Chrome implements packed integer dot products on all devices.
You can use these features in Chrome Stable today to achieve better performance.
Proposed features
Looking forward, we're investigating two more features: subgroups and cooperative matrix multiply.
The subgroups feature enables SIMD-level parallelism to communicate or to perform collective math operations, such as a sum for more than 16 numbers. This allows for efficient cross-thread data sharing. Subgroups are supported on modern GPUs APIs, with varying names and in slightly different forms.
We've distilled the common set into a proposal that we've taken to the WebGPU standardization group. And, we've prototyped subgroups in Chrome behind an experimental flag, and have brought our initial results into the discussion. The main issue is how to ensure portable behavior.
Cooperative matrix multiply is a more recent addition to GPUs. A large matrix multiply can be broken down into multiple smaller matrix multiplications. Cooperative matrix multiply performs multiplications on these smaller fixed-sized blocks in a single logical step. Within that step, a group of threads cooperate efficiently to compute the result.
We surveyed support in underlying GPU APIs, and plan to present a proposal to the WebGPU standardization group. As with subgroups, we expect that much of the discussion will center around portability.
To evaluate the performance of subgroup operations, in a real application, we integrated experimental support for subgroups into MediaPipe and tested it with Chrome's prototype for subgroup operations.
We used subgroups in GPU kernels of the prefill phase of the large language model, so I'm only reporting the speedup for the prefill phase. On an Intel GPU, we see that subgroups perform two-and-a-half times faster than baseline. However, these improvements aren't consistent across different GPUs.
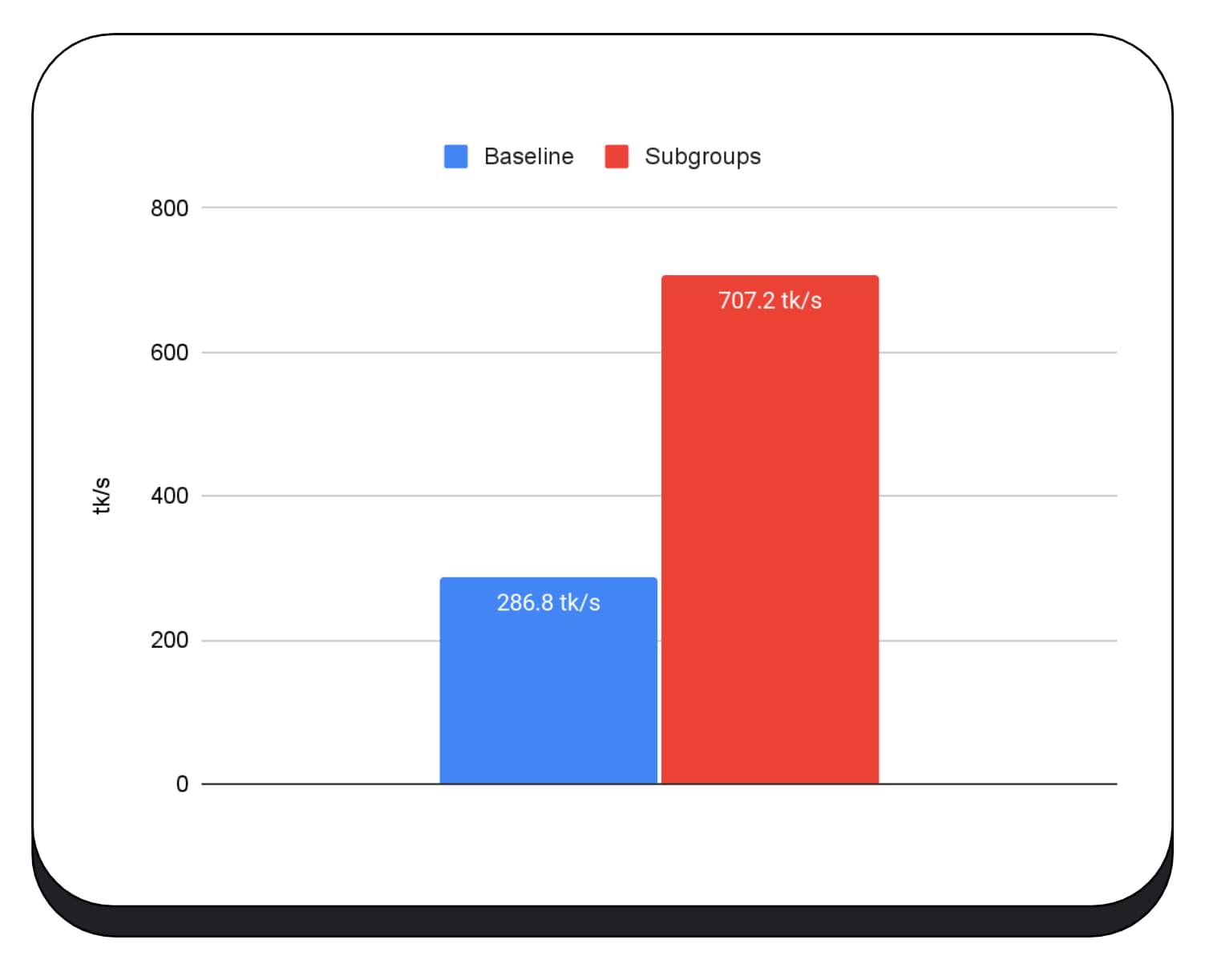
The next chart shows the results of applying subgroups to optimize a matrix multiply microbenchmark across multiple consumer GPUs. Matrix multiplication is one of the heavier operations in large language models. The data show that on many of the GPUs, subgroups increase the speed two, five, and even thirteen times the baseline. However, notice that on the first GPU, subgroups aren't much better at all.
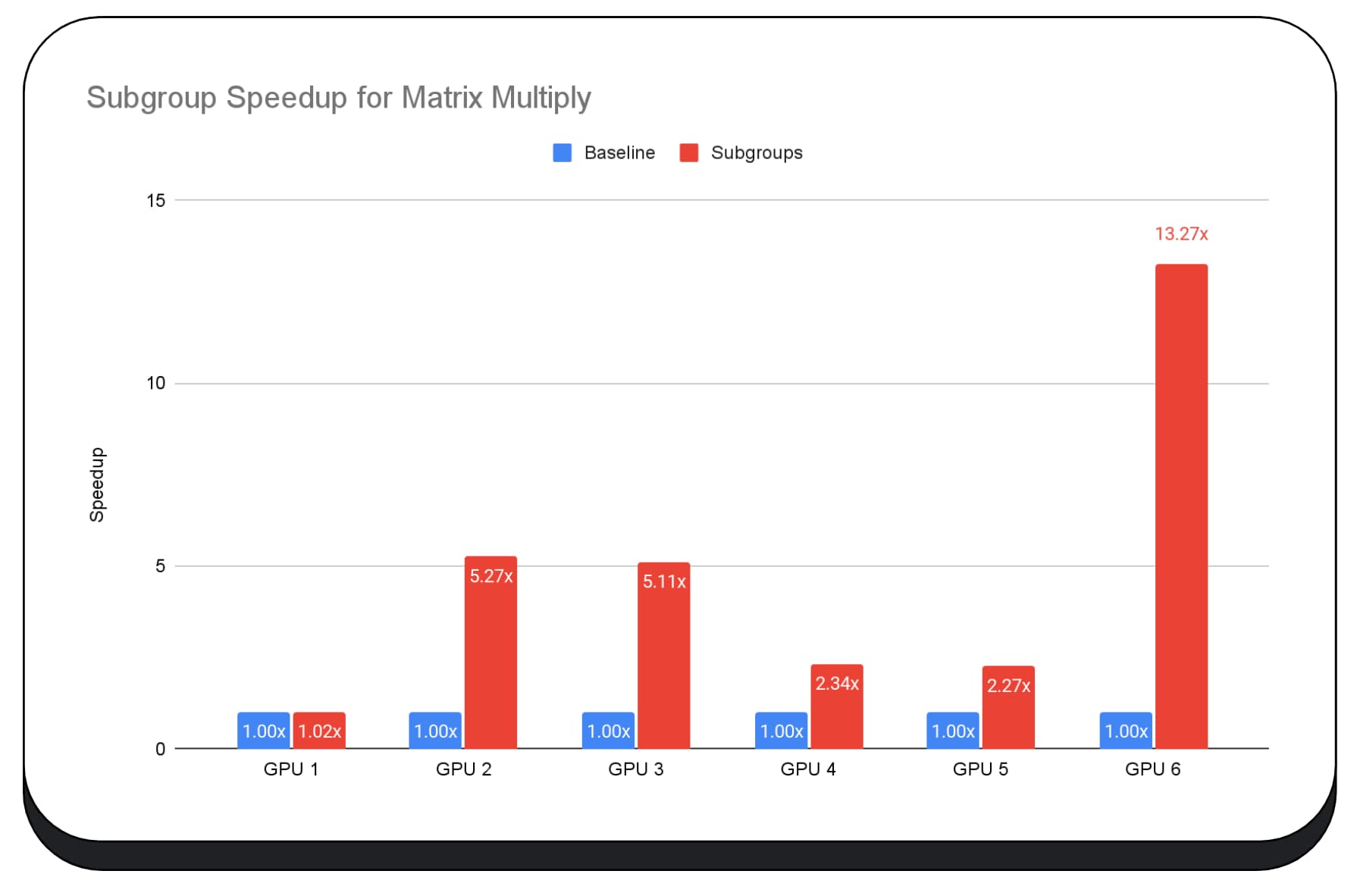
GPU optimization is difficult
Ultimately, the best way to optimize your GPU is dependent on what GPU the client offers. Using fancy new GPU features doesn't always pay off they way you might expect, because there can be lots of complex factors involved. The best optimization strategy on one GPU may not be the best strategy on another GPU.
You want to minimize memory bandwidth, while fully using the computing threads of the GPU.
Memory access patterns can be really important, too. GPUs tend to perform far better when the compute threads access memory in a pattern that is optimal for the hardware. Important: You should expect different performance characteristics on different GPU hardware. You may need to run different optimizations depending on the GPU.
In the following chart, we've taken the same matrix multiply algorithm, but added another dimension to further demonstrate the impact of various optimization strategies, and the complexity and variance across different GPUs. We've introduced a new technique here, which we'll call "Swizzle." Swizzle optimizes the memory access patterns to be more optimal for the hardware.
You can see that the memory swizzle has a significant impact; it's sometimes even more impactful than subgroups. On GPU 6, swizzle provides a 12x speedup, while subgroups provide a 13x speedup. Combined, they have an incredible 26x speedup. For other GPUs, sometimes swizzle and subgroups combined perform better than either one alone. And on other GPUs, exclusively using swizzle performs the best.
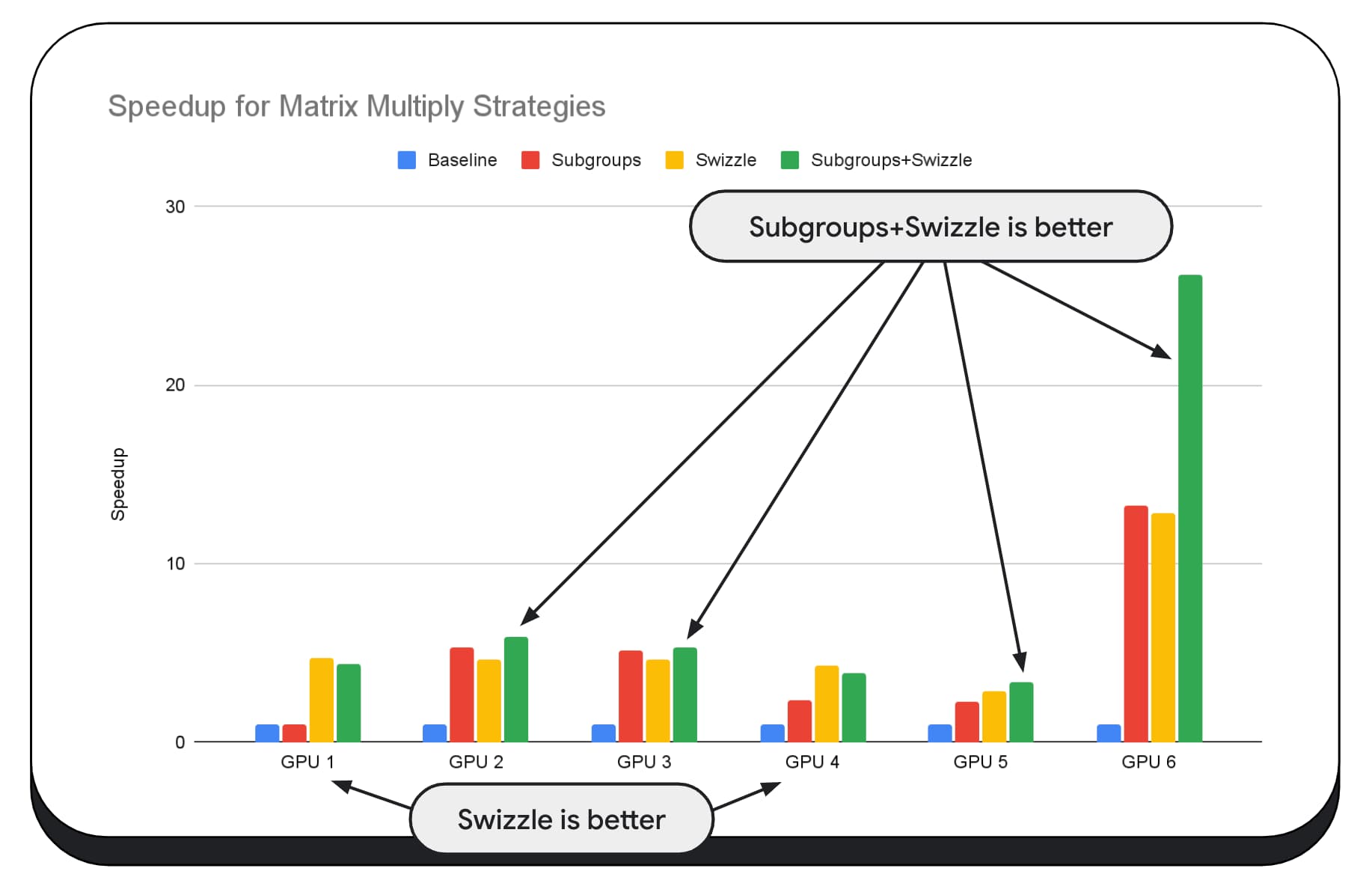
Tuning and optimizing GPU algorithms to work well on every piece of hardware, can require a lot of expertise. But thankfully there is a tremendous amount of talented work going into higher level libraries frameworks, like Mediapipe, Transformers.js, Apache TVM, ONNX Runtime Web, and more.
Libraries and frameworks are well-positioned to handle the complexity of managing diverse GPU architectures, and generating platform-specific code that will run well on the client.
Takeaways
The Chrome team continues to help evolve the WebAssembly and WebGPU standards to improve the web platform for machine learning workloads. We're investing in faster compute primitives, better interop across web standards, and making sure that models both large and small are able to run efficiently across devices.
Our goal is to maximize capabilities of the platform while retaining the best of the web: it's reach, usability, and portability. And we're not doing this alone. We're working in collaboration with the other browser vendors at W3C, and many development partners.
We hope you remember the following, as you work with WebAssembly and WebGPU:
- AI inference is available now on the web, across devices. This brings the advantage of running on client devices, such as reduced server cost, low latency, and increased privacy.
- While many features discussed are relevant primarily to the framework authors, your applications can benefit without much overhead.
- Web standards are fluid, and evolving, and we are always looking for feedback. Share yours for WebAssembly and WebGPU.
Acknowledgements
We'd like to thank the Intel web graphics team, who were instrumental in driving the WebGPU f16 and packed integer dot product features. We'd like to thank the other members of the WebAssembly and WebGPU working groups at W3C, including the other browser vendors.
Thank you to the AI and ML teams both at Google and in the open source community for being incredible partners. And of course, all of our teammates who make all of this possible.



